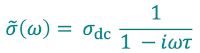Oggi parliamo di un modello molto importante per spiegare la conduzione elettrica: il modello di Drude.
Ho intenzione di presentarlo in una maniera puramente divulgativa, senza dunque approfondire nozioni e formule estremamente tecniche, in modo che anche il lettore non esperto di fisica possa farsi un'idea generale circa l'interessante argomento.
Prima di tutto specifichiamo che nella nostra breve narrazione ci soffermeremo sui metalli.
Tutti più o meno abbiamo un'idea di cosa sia un metallo, ma sareste in grado di darne una definizione fisicamente rigorosa in una singola frase?
Ok, cerchiamo di capire un po' meglio.
Innanzitutto osservate il seguente grafico, relativo nello specifico all'argento, tratto dal testo Optical Properties of Solids di Mark Fox.
Potete constatare come nella zona dell'infrarosso (dello
spettro elettromagnetico) la riflettività sia altissima (quasi il 100%) e pure nella luce visibile essa resti elevata (sopra l'80%), mentre improvvisamente cala notevolmente nell'ultravioletto.
Ed attenzione perché questo andamento della riflettività non si riscontra solo nell'argento, ma è un andamento generale caratteristico di tutti i metalli convenzionali.
Benissimo, ma cosa significa invece banda elettronica parzialmente occupata?
Beh, quando entriamo nel contesto della
fisica della materia condensata, siamo soliti classificare i materiali in
3 fondamentali categorie in base alla loro struttura in bande elettroniche:
1) metalli;
2) isolanti;
3) semiconduttori.
Grazie a
Wikipedia osserviamo a tal proposito la seguente immagine illustrativa.
Potete vedere chiaramente che negli isolanti e nei semiconduttori abbiamo uno spazio vuoto tra le bande (il cosiddetto "band gap") più o meno ampio; la banda più in basso (detta banda di valenza) è totalmente occupata da elettroni, mentre quella più in alto (banda di conduzione) potrebbe venir occupata grazie a meccanismi di eccitazione (non entreremo nei dettagli tecnici di questo fenomeno).
Nei metalli, al contrario, non abbiamo alcun band gap e, nello specifico, abbiamo una banda che si ritrova ad essere parzialmente piena di elettroni e parzialmente vuota!
Ottimo, ora potete dire ai vostri amici di sapere cosa sia davvero un metallo secondo la fisica!
Specifichiamo che l'elettrodinamica dei metalli è dovuta a 2 meccanismi diversi di transizione:
1) transizioni intrabanda: transizioni di elettroni che interessano solo la banda parzialmente occupata;
2) transizioni interbanda: transizioni di elettroni che interessano bande diverse.
Il modello di Drude è intimamente legato alla prima categoria di transizioni, che sono anche, in generale, le più rilevanti per un metallo, mentre le transizioni interbanda sono più interessanti quando parliamo di semiconduttori ed isolanti.
Altra cosa che va specificata sin da subito è che il modello di Drude è un modello classico, nel senso che non fa uso della meccanica quantistica!
In verità una sua importante estensione, il cosiddetto
modello di Drude-Sommerfeld, introdotto dal fisico tedesco Arnold Sommerfeld nel
1927, coinvolge la fisica quantistica (in particolare la
statistica di Fermi-Dirac e il concetto di
superficie di Fermi).
L'altro grande modello classico che cerca di illustrare concetti come la conducibilità elettrica e la
funzione dielettrica (in particolare nel contesto delle transizioni interbanda) è il
modello di Lorentz, proposto dal fisico olandese Hendrik Antoon Lorentz in un articolo del
1909, basato sulla fantasiosa ma efficace idea di considerare gli elettroni alla stregua di
oscillatori armonici smorzati (insomma molle!).
Si guardi a tal proposito la seguente immagine illustrativa tratta da
Wikipedia.
Ma torniamo al protagonista del nostro post, il modello di Drude.
Esso venne proposto dal fisico tedesco Paul Drude in un anno decisamente memorabile: il 1900.
Nel suddetto anno egli pubblicò infatti l'articolo denominato Zur Elektronentheorie der Metalle, pubblicazione che avvenne sulla prestigiosa rivista scientifica Annalen der Physik, sì proprio quella ove 5 anni dopo Einstein avrebbe rivoluzionato il mondo della fisica (e non solo) con magistrali contributi, tra cui l'introduzione della teoria della relatività ristretta.
Ma qual è l'ipotesi fondamentale alla base del modello di Drude?
Se per il modello di Lorentz tale ipotesi consiste nel considerare gli elettroni come molle, con Drude assumiamo invece che il nostro metallo sia un gas pieno di elettroni liberi e visti come particelle classiche, perfettamente distinguibili.
Tali elettroni si muovono in modo casuale con una certa velocità lungo linee rette fino a quando non avvengono collisioni. Per semplicità il modello va ad ignorare qualsiasi altro tipo di interazione.
Adesso viene il bello: immaginiamo di sottoporre il nostro gas di elettroni all'azione di un campo elettrico esterno.
Cosa succede? Innanzitutto abbiamo una variazione della quantità di moto (chiamata anche momento lineare) $\vec{p}$ del singolo elettrone nel sistema (ricordiamo che la quantità di moto è il prodotto della massa per la velocità del corpo) dovuta al campo elettrico applicato $\vec{E}$.
Ma abbiamo pure un importante
meccanismo di dissipazione di $\vec{p}$ dovuto alle collisioni di questi elettroni con impurezze/difetti cristallini,
fononi, altri elettroni, ecc.
Volete un modo sintetico per esprimere tutto ciò? "Facile", basta ricorrere ad un po' di matematica.
Osserviamo infatti attentamente la seguente equazione del moto alla base del modello di Drude:
Chi è abituato al formalismo matematico tipico di questo blog sa bene che a sinistra dell'uguale abbiamo la derivata del momento lineare $\vec{p}$ rispetto al tempo.
Per chi non è avvezzo al calcolo infinitesimale, possiamo semplificare la questione asserendo che si tratta di una variazione nel tempo del momento lineare di un singolo elettrone che stiamo prendendo in considerazione.
A destra dell'uguale abbiamo innanzitutto la forza (nello specifico il termine $-e \vec{E}$, dove $e$ è la carica elettrica fondamentale, cioè quella dell'elettrone) che agisce sul nostro elettrone dovuta al campo elettrico esterno; poi abbiamo un altro termine, ossia $- \frac{\vec{p}}{\tau}$, che rappresenta una forza di
attrito viscoso.
In particolare, $\tau$ è il cosiddetto tempo di rilassamento, cioè il tempo medio che intercorre tra 2 collisioni o, in altre parole, la quantità che governa il rilassamento del sistema verso l'equilibrio (condizione in cui la quantità di moto media è 0), dopo che è stato rimosso il nostro fattore perturbativo esterno (cioè il campo elettrico).
E chiaramente l'introduzione di un campo elettrico esterno ha conseguenze pure sulla velocità delle particelle.
Infatti si va a definire la cosiddetta velocità di deriva
dove $m$ indica la massa dell'elettrone.
La cosa importante da notare è che la suddetta velocità mantiene la direzione del campo elettrico $\vec{E}$ ma presenta verso opposto (specificato da quel segno $-$ nell'ultima equazione).
Con un po' di passaggi matematici, tra cui assumere il campo elettrico come alternato e ricordare la celebre
legge di Ohm (generalizzata), grazie a tutte queste considerazioni uno può giungere alla quantità fisica protagonista del modello di Drude: la
conducibilità elettrica $\tilde{\sigma}$.
Di seguito l'espressione matematica che la definisce:
Notiamo immediatamente che tale quantità è fornita dal prodotto della cosiddetta
conducibilità in corrente continua, $\sigma_{dc}$, e di un termine frazionario che coinvolge la
frequenza angolare $\omega$ relativa al campo $\vec{E}$, il tempo di rilassamento $\tau$ e l'unità immaginaria $i$ (
cliccate qui per dettagli sull'unità immaginaria e i numeri complessi).
Nota per il lettore non esperto: a sinistra dell'uguale le parentesi tonde con dentro $\omega$ non indicano una moltiplicazione, ma semplicemente il fatto che la conducibilità $\tilde{\sigma}$ ha una dipendenza esplicita dalla frequenza $\omega$.
Tuttavia l'aspetto essenziale è il seguente: $\tilde{\sigma}$ è una quantità complessa, dunque scomponibile in una somma di una parte reale $\sigma_1$ e di una parte immaginaria $\sigma_2$, ovvero in simboli:
Ora chiaramente $\sigma_1$ e $\sigma_2$ possono essere espresse da precise relazioni matematiche, ma l'aspetto più interessante è osservare il comportamento di tali quantità rispetto alla frequenza.
A tal proposito guardate la seguente figura.
Potete notare come la parte reale ed immaginaria della conducibilità elettrica siano rappresentate da curve diverse e, in particolare, se andiamo a vedere cosa succede quando la frequenza tende a 0, possiamo constatare che $\sigma_1$ tende ad un certo valore che è nient'altro che $\sigma_{dc}$, mentre $\sigma_2$ tende a 0.
Ottimo, ora avete un'idea generale di come si comporta la conducibilità elettrica nei metalli assumendo un modello ideale come quello di Drude.
Dovrebbe poi essere cosa nota che i metalli che sono buoni conduttori di elettricità siano pure buoni conduttori di calore (pensate per esempio all'utilizzo delle pentole con fondo in rame nella cucina).
Ebbene, grazie al modello di Drude-Sommerfeld è possibile dimostrare matematicamente (state tranquilli, non lo faremo qui) una legge sperimentale, scoperta nel 1853, che mette in relazione la conducibilità elettrica $\sigma$ e la conducibilità termica $\kappa_T$: la legge di Wiedemann-Franz.
Nella sua forma più semplice e compatta essa si presenta nel modo seguente:
$\frac{\kappa_T}{\sigma} = LT$
Qui $T$ denota ovviamente la temperatura, mentre $L$ è il cosiddetto numero di Lorenz (scoperto da Ludvig Lorenz nel 1872), una quantità indipendente dal tipo di metallo che viene considerato nelle misurazioni.
A mo' di conclusione, vorrei far notare come nel 2006 un duo di scienziati, Martin Dressel e Marc Scheffler, abbia condotto un'interessante verifica moderna della validità del modello di Drude.
Di seguito l'abstract dell'articolo, pubblicato non a caso su Annalen der Physik.
Cerco di riassumervi in poche e semplici parole gli aspetti cruciali del suddetto articolo.
Innanzitutto i 2 scienziati hanno osservato come in un regime di frequenza bassa (il nome rigoroso è regime di Hagen-Rubens) misure di riflettività siano state eseguite solamente nei cosiddetti "metalli cattivi", come l'acciaio inossidabile.
La caratteristica essenziale dei "metalli cattivi" è il fatto che presentino un valore basso di $\sigma_{dc}$ ed un valore elevato del rapporto $\frac{1}{\tau}$.
Ne consegue sostanzialmente che la loro riflettività devia molto dal 100% persino in un regime di bassa frequenza; andate per favore a rivedervi all'inizio del post cosa succedeva nel caso dell'argento, ove invece la riflettività era elevatissima nelle basse frequenze (o, equivalentemente, nelle larghe lunghezze d'onda dello spettro elettromagnetico).
Dressel e Scheffler hanno poi riscontrato un problema spinoso: solo nel regime delle microonde e di frequenze di pochi terahertz è possibile misurare la parte reale e la parte immaginaria di $\tilde{\sigma}$ in modo indipendente, tuttavia per i metalli convenzionali il fondamentale rapporto $\frac{1}{\tau}$ è ben al di sopra di tali frequenze!
Una possibile soluzione iniziale è stata quella di osservare cosa succede in semiconduttori moderatamente drogati.
No, non stiamo incentivando all'uso delle sostanze stupefacenti; il termine "drogato" (o, volendo, "doping") nell'ambito dei semiconduttori significa semplicemente che stiamo applicando un certo meccanismo che aumenta il numero di portatori di carica di quel semiconduttore, rendendolo così più simile ad un metallo in termini di conducibilità elettrica di quanto lo fosse originariamente.
Ed effettivamente l'uso del doping ha fornito (nel caso specifico dell'articolo si è fatto riferimento al silicio leggermente drogato) risultati sperimentali in accordo col modello teorico di Drude!
Ma non è finita qui, perché i 2 scienziati hanno giustamente evidenziato che se volessimo dati migliori dovremmo lavorare nel range di frequenze delle
microonde.
E per far ciò si sono dovuti attenere ad una teoria più complessa, la
teoria del liquido di Fermi, introdotta dal famoso fisico russo Lev Landau nel
1956.
Senza entrare nei complicati dettagli, ciò che è rilevante sapere è che tale teoria si applica stupendamente a particolari materiali intermetallici, i cosiddetti
composti di fermioni pesanti.
Dressel e Scheffler hanno pertanto considerato uno di questi composti, chiamato $\mathrm{UPd_2Al_3}$, compiendo analisi in un range di frequenze vastissimo, nello specifico da 50 MHz a 40 GHz, focalizzandosi su temperature vicine allo
zero assoluto, in particolare sopra 1.6 kelvin.
Il finale della storia forse è scontato, ma non toglie nulla alla meraviglia di un'importante rilevazione scientifica: anche nel suddetto caso i dati sperimentali hanno confermato un'ottima corrispondenza con il modello teorico di Drude!
Insomma, il duo di scienziati, poco più di 100 anni dopo la formulazione originaria del modello di Drude, ha dimostrato che tale modello, per quanto basilare, è ancora molto buono, in certi regimi di frequenza, nel descrivere il comportamento generale della conducibilità elettrica in metalli e materiali che si avvicinano alle caratteristiche dei metalli.
Ovviamente moderne tecniche più sofisticate fondate sulla meccanica quantistica, come l'approccio a molti elettroni sviluppato dal danese
Jens Lindhard nel
1954 basandosi sulla cosiddetta
Random-Phase Approximation, portano a risultati più rigorosi in generale.
I lettori esperti interessati possono trovare,
cliccando qui, un interessantissimo articolo di Andrade-Neto in cui si mette a diretto confronto il modello di Drude con il più avanzato modello di Lindhard.
----------------------------------------------------------------------------------------
Fonti essenziali:
- Optical Properties of Solids di M. Fox
- Electrodynamics of Solids di M. Dressel e G. Grüner
- Verifying the Drude Response di M. Dressel e M. Scheffler




.png)